算法之道（1）基础

2017-01-17

前言：

算法的基础是数学。高等代数、线性代数、离散数学的知识显得十分重要。

一、算法简介

1、算法，是任何良定义的计算过程，某个值或集合输入，产生某个值或集合的输出。

2、算法，可以看成一种技术。计算机也许是快的，但它们不是无限快。存储器也许是廉价的，但不是免费的。因此算法帮助我们有效的使用时间或空间等资源。

3、学习已有的算法，是为了深层理解算法设计与分析的技术，以便能自行设计算法，证明其正确性和理解其效率。

二、算法分析-时间复杂度

我们以插入排序的算法为例，解释时间复杂度计算。

def insertion_sort2(list):          # 代价  次数
    for j in range(1,len(list)):    # c1    n (循环头会比循环体多执行1次)
        key =list[j]                # c2    n-1
        i=j-1                       # c4    n-1
        while i>=0 and list[i]>key: # c5    t(1)+t(2)+t(3)+...+t(j)，t(j)表示当值为j时循环次数，t(j)最坏情况执行j+1次，t(1)=2,t(2)=3,t(n-1)=n，最好情况执行1次。
            list[i+1]=list[i]       # c6    t(1)-1 + t(2)-1 +... t(j)-1，t(j)-1最坏情况执行j次，最好情况执行0次
            i=i-1                   # c7    t(1)-1 + t(2)-1 +... t(j)-1，同上一行
        list[i+1]=key               # c8    n-1
        print(list)
    return list

numbers = [12, 123, 23, 232, 9, 11, 7]
insertion_sort(numbers)

T(n)=c_1n+c_2(n-1)+c_4(n-1)+c_5\sum_{j=1}^{n-1}t_j+c_6\sum_{j=1}^{n-1}(t_j-1)+c_7\sum_{j=1}^{n-1}(t_j-1)+c_8(n-1)

最佳情况运行时间，可以看出是n的线性函数。

T(n)=c_1n+c_2(n-1)+c_4(n-1)+c_5(n-1)+c_8(n-1)

=(c_1+c_2+c_4+c_5+c_8)n-(c_2+c_4+c_5+c_8)

最坏情况运行时间：

\sum_{j=1}^{n-1}(t_j)=\dfrac{n(n+1)}{2}-1

还有：

\sum_{j=1}^{n-1}(t_j-1)=\dfrac{n(n-1)}{2}

得出是n的二次函数。

T(n)=(\dfrac{c_5}{2}+\dfrac{c_6}{2}+\dfrac{c_7}{2})n^2+(c_1+c_2+c_4+\dfrac{c_5}{2}-\dfrac{c_6}{2}-\dfrac{c_7}{2}+c_8)n-(c_2+c_4+c_5+c_8)

我们往往只求最坏情况运行时间，原因在于，

一个算法的最坏情况运行时间给出了任意输入的运行时间的上界，不会变的更坏。
对某些算法，最坏情况经常出现。
平均情况往往与最坏情况大致一样差。

三、分治法（Divide and Conquer）

许多算法结构上是递归的，遵循分治法的思想：将原问题分解为几个规模较小但类似于原问题的子问题，递归地求解这些子问题，然后再合并这些子问题的解来建立原问题的解。

分治模式在每层递归时有三个步骤：分解、解决、合并。

分治算法运行时间的递归式为：T(n)是规模为n的一个问题的运行时间，如问题规模足够小，当n<=c（某个常量）时，直接求解需要常量时间，协作 $\Theta(1)$ 。把原问题分解成a个子问题，每个子问题的规模是原问题的1/b（对归并排序，a和b都为2）。为了求解子问题，需要T(n/b)的时间，分解问题需要的时间D(n)，合并子问题需要的时间C(n)，则可得到递归式：

T(n)= \begin{cases} \Theta(1) &\text{if } n \le c \\ aT(n/b)+D(n)+C(n) &\text{if } n>c \end{cases}

具体到递归排序，分解运行时间如下：

分解：D(n)= $\Theta(1)$ 。
解决：2T(n/2)
合并：C(n)= $\Theta(n)$ 。

递归排序的最坏运行时间T(n)的递归式：

T(n)= \begin{cases} c &\text{if } n=1 \\ 2T(n/2)+cn &\text{if } n>1 \end{cases}

递归式求解如下：

第一层为1个cn，第二层为2个2/cn，第lgn层为n个c，因此递归式总体运行时间为cn lgn+cn。

四、函数的增长

Θ记号

我们已经使用过渐进记号 $\Theta$ 来表示增长量级，该记号适用于函数，例如插入排序的运行时间： $\Theta(n^2)=an^2+bn+c$

对于给定的函数g(n)，表示以下函数的集合：

\Theta(g(n))

={f(n)：存在正常量

c_1,c_2,n_0

，使得对所有

n \ge n_0

，有

0 \le c_1g(n) \le f(n) \le c_2g(n)

}

O记号

Theta记号渐进给出一个函数的上界和下界。当只有一个渐进上界时，使用O记号。用来表示以下函数的集合：
O(g(n))={f(n)：存在正常量 $c,n_0$ ，使得对所有 $n \ge n_0$ ，有 $0 \le f(n) \le cg(n)$ }

按数量级递增排列，常见的时间复杂度有：常数阶O(1),对数阶O(lgn),线性阶O(n), 线性对数阶O(nlgn),平方阶O(n^2)，立方阶O(n^3)… k次方阶O(n^k),指数阶O(2^n)。随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低。

Ω记号

提供函数的渐进下界。

五、算法基础

贝塞尔曲线

下面我们就通过例子来了解一下如何用 de Casteljau 算法绘制一条贝塞尔曲线。

在平面内任选 3 个不共线的点，依次用线段连接。

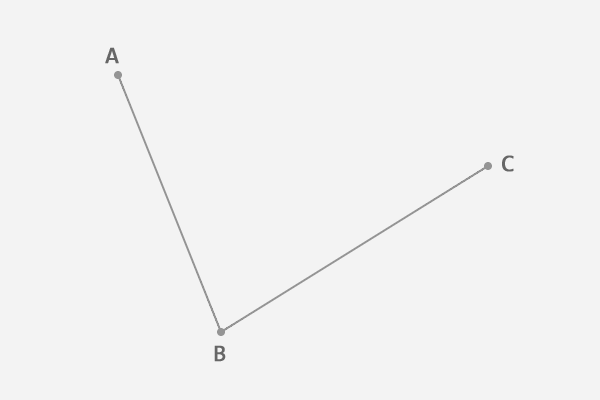
在第一条线段上任选一个点 D。计算该点到线段起点的距离 AD，与该线段总长 AB 的比例。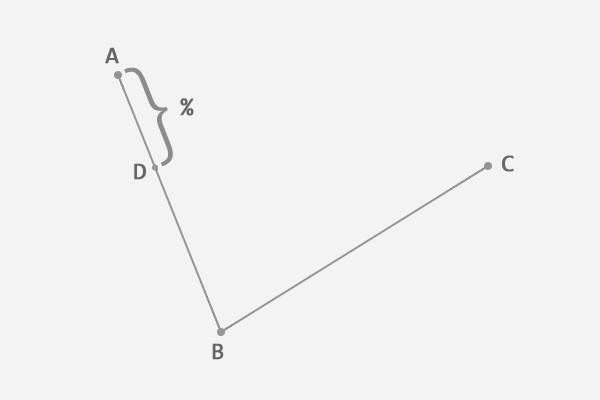

根据上一步得到的比例，从第二条线段上找出对应的点 E，使得 AD:AB = BE:BC。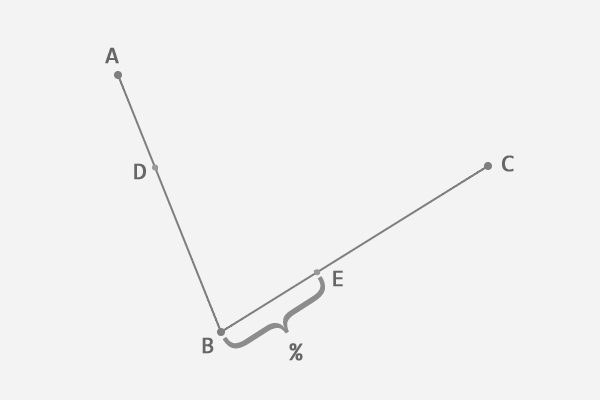

连接这两点 DE。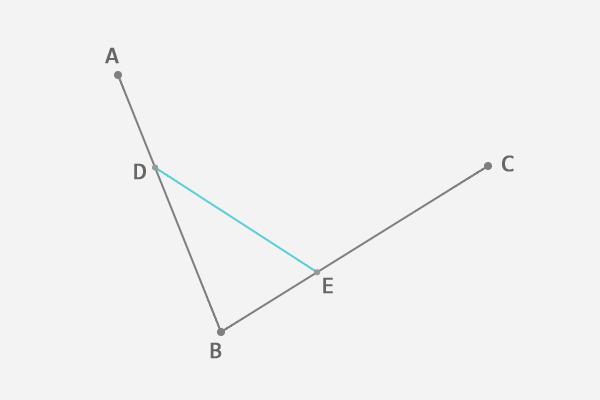

从新的线段 DE 上再次找出相同比例的点 F，使得 DF:DE = AD:AB = BE:BC。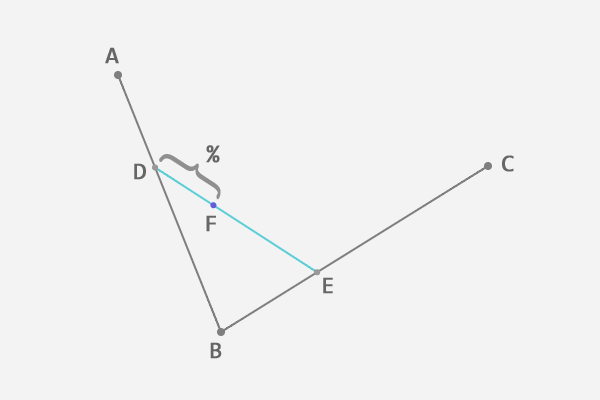

到这里，我们就确定了贝塞尔曲线上的一个点 F。接下来，请稍微回想一下中学所学的极限知识，让选取的点 D 在第一条线段上从起点 A 移动到终点 B，找出所有的贝塞尔曲线上的点 F。所有的点找出来之后，我们也得到了这条贝塞尔曲线。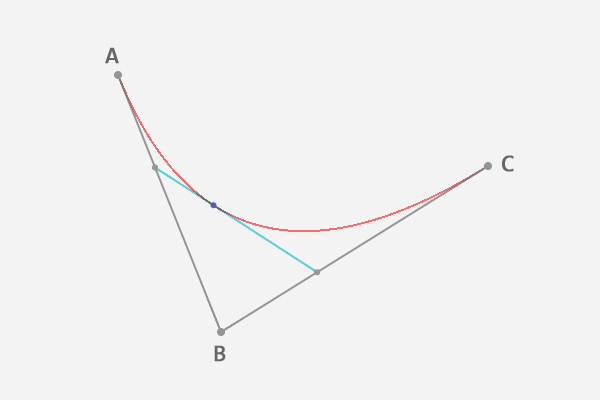

如果你实在想象不出这个过程，没关系，看动画！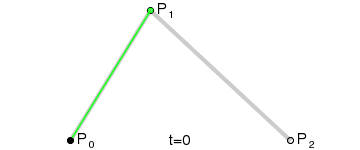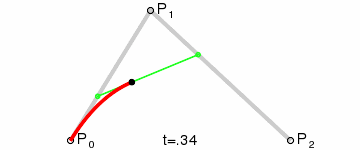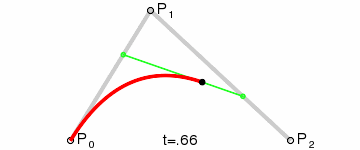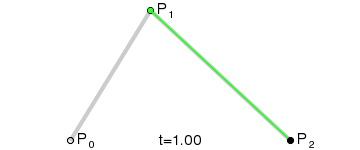

回过头来看这条贝塞尔曲线，为了确定曲线上的一个点，需要进行两轮取点的操作，因此我们称得到的贝塞尔曲线为二次曲线（这样记忆很直观，但曲线的次数其实是由前面提到的伯恩斯坦多项式决定的）。

当控制点个数为 4 时，情况是怎样的？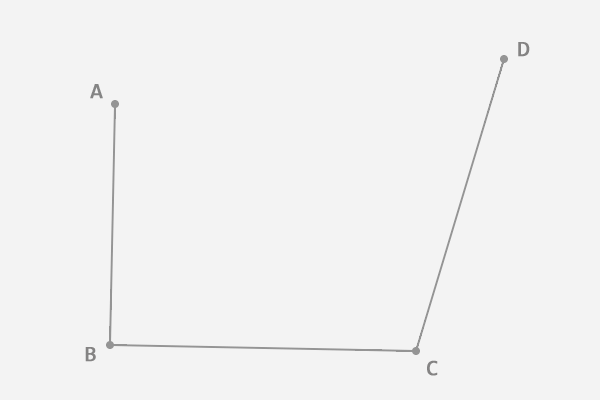
步骤都是相同的，只不过我们每确定一个贝塞尔曲线上的点，要进行三轮取点操作。如图，AE:AB = BF:BC = CG:CD = EH:EF = FI:FG = HJ:HI，其中点 J 就是最终得到的贝塞尔曲线上的一个点。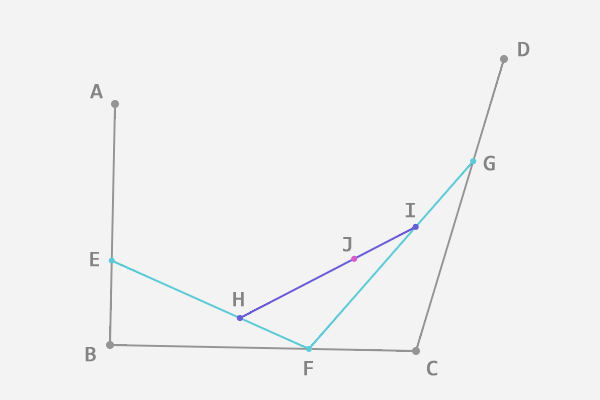
这样我们得到的是一条三次贝塞尔曲线。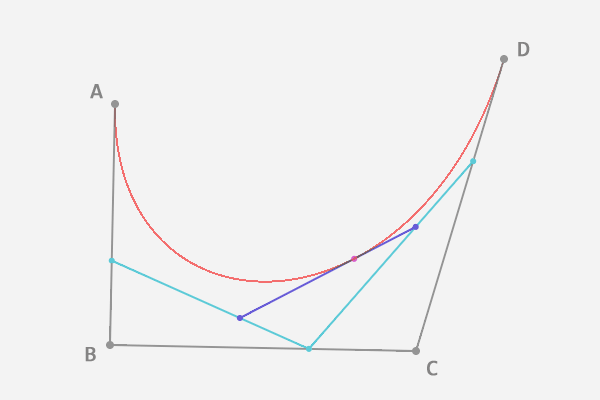
看过了二次和三次曲线，更高次的贝塞尔曲线大家应该也知道要怎么画了吧。那么比二次曲线更简单的一次（线性）贝塞尔曲线存在吗？长什么样？根据前面的介绍，只要稍作思考，想必你也能猜出来了。哈！就是一条直线~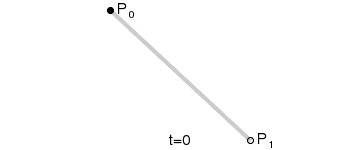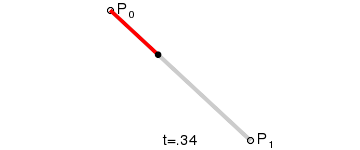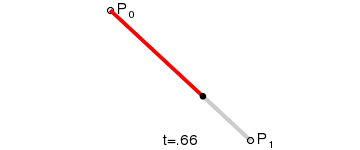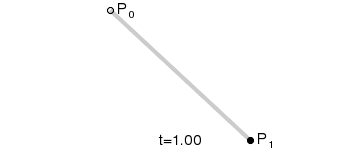

能画曲线也能画直线，是不是很厉害？要绘制更复杂的曲线，控制点的增加也仅仅是线性的。这一特点使其不光在工业设计领域大展拳脚，就连数学基础不好的人也可以比较容易地掌握，比如大多数平面美术设计师们。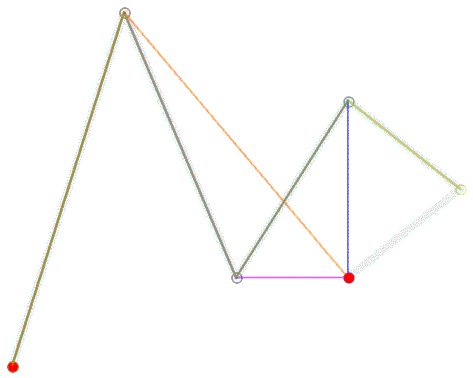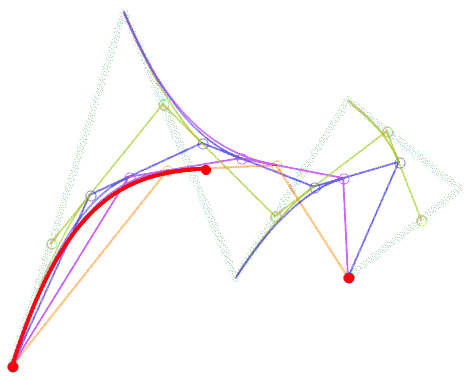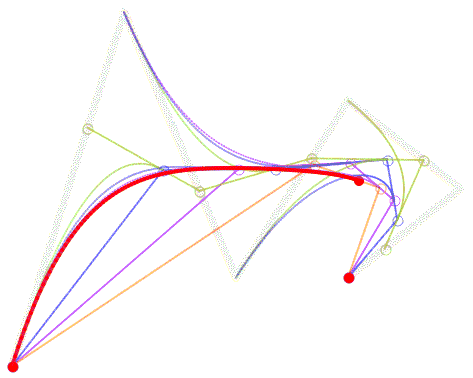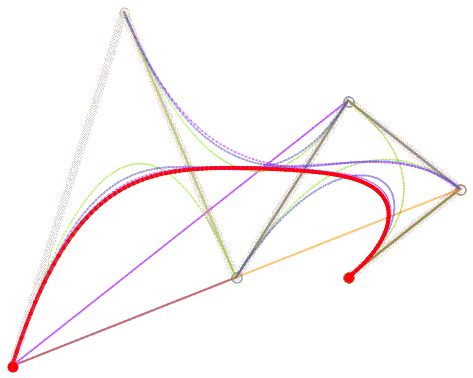

上面介绍的内容并不足以展示贝塞尔曲线的真正威力。推广到三维空间的贝塞尔曲面，以及更进一步的非均匀有理 B 样条（NURBS），早已成为当今计算机辅助设计（CAD）的行业标准，不论是我们平常用到的各种产品，还是在电影院看到的精彩大片，都少不了它们的功劳。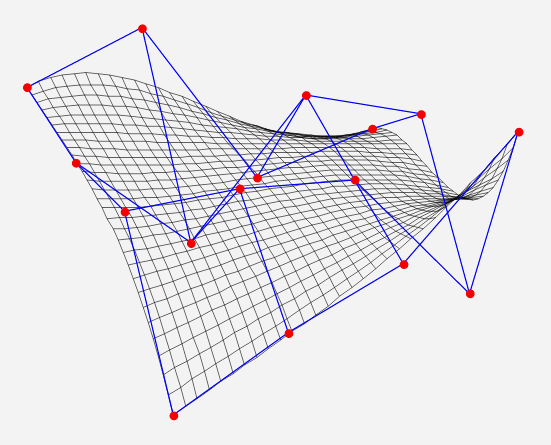

未完待续……