机器学习（5）线性回归

一、线性回归

回归

回归是监督学习的一个重要问题，回归用于预测输入变量和输出变量之间的关系，目的是预测数值型的目标值。
回归模型（回归方程）是表示输入变量到输出变量之间映射的函数。
回归问题的学习等价于函数拟合：使用一条函数曲线使其很好的拟合已知函数且很好的预测未知数据。

回归问题分为模型的学习和预测两个过程。基于给定的训练数据集构建一个模型，根据新的输入数据预测相应的输出。

回归问题按照输入变量的个数可以分为一元回归和多元回归；
按照输入变量和输出变量之间关系的类型，可以分为线性回归和非线性回归。如果你和的线是一条直线，则被称为线性回归。非线性回归有常用的逻辑回归模型。

线性回归

一元线性回归最简单：y=ax+b(x为价格，y为销量，则该线性回归用来描述价格与销量的关系，一元代表输入只有一个维度-价格，求a和b的值)

多元回归，代表输入有多个维度。

可以用最小二乘法，梯度下降法求解线性预测函数的系数

逻辑回归（logistic ）

逻辑回归的模型是一个非线性模型，它本质上又是一个线性回归模型，因为通过sigmoid映射函数（又称逻辑回归函数）关系，转换成线性回归问题来解决。

二、最小二乘法

最小二乘法适用于任意多维度的线性回归参数求解，它可求解出一组最优解，使得对于样本集中的每一个样本，用y=f(x1,x2,…xi,…xn)来预测样本，使得预测值与实际值的方差最小。

模型公式

hθ(x)=∑i=0mθixi=θTX h_{\theta}(x) = \sum_{i=0}^m{\theta_i x_i}=\theta^T X

θ和X都是列向量。

目标函数（损失函数）

根据最小二乘法定义，目标函数表示是预测值和真实值的差距。

J(θ)=12∑i=0m(hθ(xi)−yi)2 J(\theta) = \dfrac{1}{2} \sum_{i=0}^m (h_{\theta}(x_i)-y_i)^2

直观的理解，为了避免正负抵消，是每个样本值与全体样本值的平均数之差的平方，和方差类似。如通过模型函数推导，较为复杂：

多维参数的数学推导

首先模型函数包含噪音项，根据中心极限定理，满足均值为0的高斯分布

εi∼N(0,σ2) \varepsilon_i \sim N(0,\sigma^2)

有：

εi=yi−θTxi \varepsilon_i =y_i-\theta^T x_i

高斯分布表示如下：

p(yi∣xi;θ)=12πσe(−(yi−θTxi)22σ2) p(y_i|x_i;\theta)=\dfrac{1}{\sqrt{2\pi}\sigma}e^{(- \dfrac{(y_i-\theta^T x_i)^2}{2\sigma^2})}

通过极大似然MLE求得似然函数为所有样本的乘积

L(θ)=∏i=1mp(yi∣xi;θ)=∏i=1m12πσe(−(yi−θTxi)22σ2) L(\theta) = \prod_{i=1}^m p(y_i|x_i;\theta) = \prod_{i=1}^m \dfrac{1}{\sqrt{2\pi}\sigma}e^{(- \dfrac{(y_i-\theta^T x_i)^2}{2\sigma^2})}

求log，将极大似然最大值转为log函数的最大值，

l(θ)=logL(θ)=log∏i=1m12πσe(−(yi−θTxi)22σ2)=∑i=0mlog12πσe(−(yi−θTxi)22σ2) l(\theta) = \log{L(\theta)} =\log{\prod_{i=1}^m \dfrac{1}{\sqrt{2\pi}\sigma}e^{(- \dfrac{(y_i-\theta^T x_i)^2}{2\sigma^2})}} = \sum_{i=0}^m \log{\dfrac{1}{\sqrt{2\pi}\sigma}e^{(- \dfrac{(y_i-\theta^T x_i)^2}{2\sigma^2})}} =mlog12πσ−1σ212∑i=0m(yi−θTxi)2 = m \log{ \dfrac{1}{\sqrt{2\pi}\sigma}} - \dfrac{1}{\sigma^2} \dfrac{1}{2} \sum_{i=0}^m (y_i-\theta^T x_i)^2

要使得最大似然最大，则需要最小二乘最小。有：

J(θ)=12∑i=0m(hθ(xi)−yi)2=12(Xθ−y)T(Xθ−y) J(\theta) = \dfrac{1}{2} \sum_{i=0}^m (h_{\theta}(x_i)-y_i)^2 = \dfrac{1}{2} (X\theta-y)^T(X\theta-y)

得出

dJ(θ)dθ=XTXθ−XTy \dfrac{dJ(\theta)}{d\theta} = X^T X\theta-X^T y

当矩阵满秩时，求导后取极值点，令函数值为0，得出

θ=(XTX)−1XTy \theta = (X^T X)^{-1} X^T y

也可以通过贝叶斯最大后验概率进行推导。

三、线性回归实例

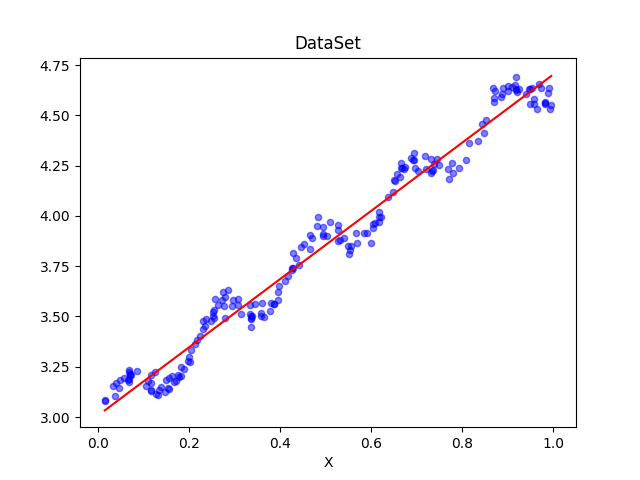
有数据如下，需要计算最优回归系数。

x0-偏移量 x1-x轴 x2-y轴
1.000000 0.067732 3.176513
1.000000 0.427810 3.816464
… … …
1.000000 0.995731 4.550095
1.000000 0.738336 4.256571
1.000000 0.981083 4.560815 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
import matplotlib.pyplot as plt

def loadDataSet(fileName):
    '''

    :param fileName: 文件名
    :return: dataMat 数据集，labelMat 标签
    '''
    numFeat = len(open(fileName).readline().split('\t')) - 1
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr =[]
        curLine = line.strip().split('\t')
        for i in range(numFeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat,labelMat

def plotDataSet():
    '''
    绘制数据集
    :return:
    '''
    xArr, yArr = loadDataSet('ex0.txt')                                    #加载数据集
    n = len(xArr)                                                        #数据个数
    xcord = []; ycord = []                                                #样本点
    for i in range(n):
        xcord.append(xArr[i][1]); ycord.append(yArr[i])                    #样本点
    fig = plt.figure()
    ax = fig.add_subplot(111)                                            #添加subplot
    ax.scatter(xcord, ycord, s = 20, c = 'blue',alpha = .5)                #绘制样本点
    plt.title('DataSet')                                                #绘制title
    plt.xlabel('X')
    plt.show()

if __name__ == '__main__':
    plotDataSet()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def standRegres(xArr, yArr):
    '''
    计算回归系数
    :param xArr:数据集
    :param yArr:标签
    :return:
    '''
    xMat = np.mat(xArr);
    yMat = np.mat(yArr).T #T方法为转置
    xTx = xMat.T * xMat  # 根据文中推导的公示计算回归系数
    if np.linalg.det(xTx) == 0.0: #奇异矩阵的性质是，其行列式的值为0
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xMat.T * yMat) # I方法为求逆
    return ws


def plotRegression():
    '''
    绘制回归曲线和数据集
    :return:
    '''
    xArr, yArr = loadDataSet('ex0.txt')  # 加载数据集
    ws = standRegres(xArr, yArr)  # 计算回归系数
    xMat = np.mat(xArr)  # 创建xMat矩阵
    yMat = np.mat(yArr)  # 创建yMat矩阵
    xCopy = xMat.copy()  # 深拷贝xMat矩阵
    xCopy.sort(0)  # 排序
    yHat = xCopy * ws  # 计算对应的y值
    fig = plt.figure()
    ax = fig.add_subplot(111)  # 添加subplot
    ax.plot(xCopy[:, 1], yHat, c='red')  # 绘制回归曲线
    ax.scatter(xMat[:, 1].flatten().A[0], yMat.flatten().A[0], s=20, c='blue', alpha=.5)  # 绘制样本点
    plt.title('DataSet')  # 绘制title
    plt.xlabel('X')
    plt.show()
    
if __name__ == '__main__':
    plotRegression()

求解出的ws回归系数为，用函数表示为：y=3.00774324+1.69532264x

1
2
[[3.00774324]
[1.69532264]]

四、局部加权线性回归

定义

局部加权线性回归（Locally Weighted Linear Regression，LWLR），是为了解决线性回归可能出现的欠拟合现象，在该方法中，我们给待预测点附近的每个点赋予一定的权重。形式如下：

θ=(XTWX)−1XTWy \theta = (X^TWX)^{-1} X^TWy

对比之前的公式，区别在于多了W，来给每个点赋予权重。LWLR使用“核”（类似于向量机的核）来对附近的点赋予更高的权重，常用的核是高斯核，k被称为平滑参数，如下：

w(i,i)=exp(∣x(i)−x∣−2k2) w(i,i)=exp(\dfrac{|x^{(i)}-x|}{-2k^2})

代码实现

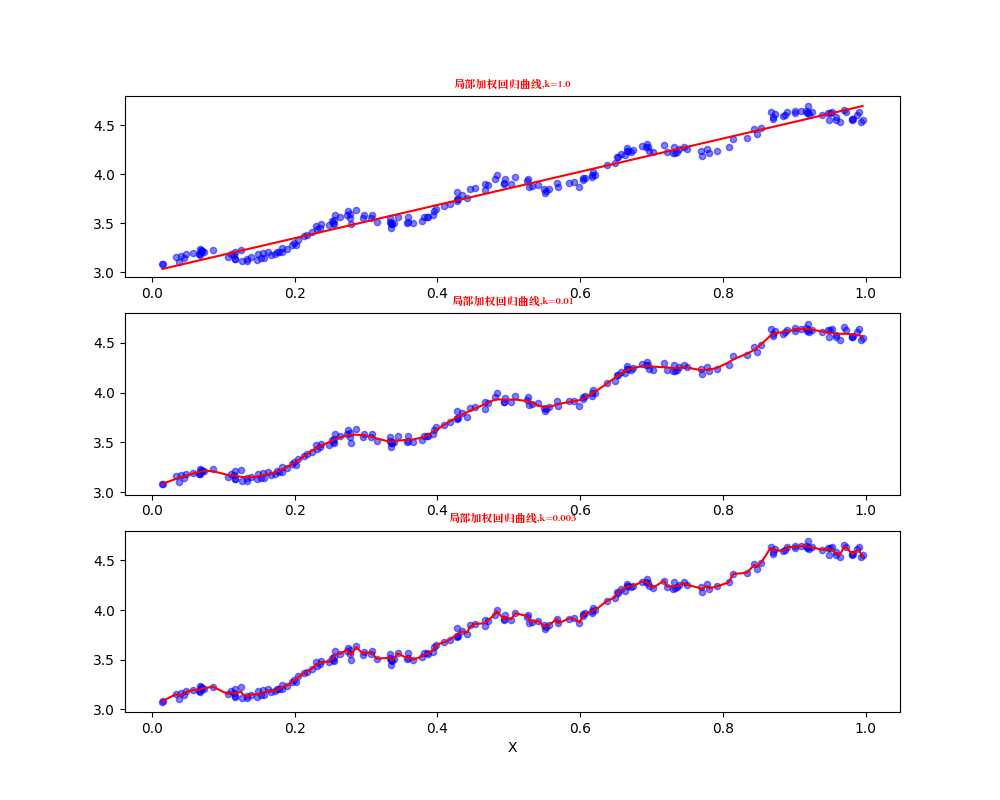
还是之前回归的数据，使用k=1，k=0.01，k=0.003进行局部加权线性回归，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
import linear_regression

def plotlwlrRegression():
    '''
    绘制多条局部加权回归曲线
    :return:
    '''
    font = FontProperties(fname=r"/Library/Fonts/Songti.ttc", size=14)
    xArr, yArr = linear_regression.loadDataSet('ex0.txt')  # 加载数据集
    yHat_1 = lwlrTest(xArr, xArr, yArr, 1.0)  # 根据局部加权线性回归计算yHat
    yHat_2 = lwlrTest(xArr, xArr, yArr, 0.01)  # 根据局部加权线性回归计算yHat
    yHat_3 = lwlrTest(xArr, xArr, yArr, 0.003)  # 根据局部加权线性回归计算yHat
    xMat = np.mat(xArr)  # 创建xMat矩阵
    yMat = np.mat(yArr)  # 创建yMat矩阵
    srtInd = xMat[:, 1].argsort(0)  # 排序，返回索引值
    xSort = xMat[srtInd][:, 0, :]
    fig, axs = plt.subplots(nrows=3, ncols=1, sharex=False, sharey=False, figsize=(10, 8))
    axs[0].plot(xSort[:, 1], yHat_1[srtInd], c='red')  # 绘制回归曲线
    axs[1].plot(xSort[:, 1], yHat_2[srtInd], c='red')  # 绘制回归曲线
    axs[2].plot(xSort[:, 1], yHat_3[srtInd], c='red')  # 绘制回归曲线
    axs[0].scatter(xMat[:, 1].flatten().A[0], yMat.flatten().A[0], s=20, c='blue', alpha=.5)  # 绘制样本点
    axs[1].scatter(xMat[:, 1].flatten().A[0], yMat.flatten().A[0], s=20, c='blue', alpha=.5)  # 绘制样本点
    axs[2].scatter(xMat[:, 1].flatten().A[0], yMat.flatten().A[0], s=20, c='blue', alpha=.5)  # 绘制样本点
    # 设置标题,x轴label,y轴label
    axs0_title_text = axs[0].set_title(u'局部加权回归曲线,k=1.0', FontProperties=font)
    axs1_title_text = axs[1].set_title(u'局部加权回归曲线,k=0.01', FontProperties=font)
    axs2_title_text = axs[2].set_title(u'局部加权回归曲线,k=0.003', FontProperties=font)
    plt.setp(axs0_title_text, size=8, weight='bold', color='red')
    plt.setp(axs1_title_text, size=8, weight='bold', color='red')
    plt.setp(axs2_title_text, size=8, weight='bold', color='red')
    plt.xlabel('X')
    plt.show()

def lwlr(testPoint, xArr, yArr, k=1.0):
    '''
    使用局部加权线性回归计算回归系数w
    :param testPoint: 测试样本点
    :param xArr: 数据集
    :param yArr: 标签y
    :param k: 高斯核的k,自定义参数
    :return: 回归系数
    '''
    xMat = np.mat(xArr);
    yMat = np.mat(yArr).T
    m = np.shape(xMat)[0]
    weights = np.mat(np.eye((m)))  # 创建权重对角矩阵
    for j in range(m):  # 遍历数据集计算每个样本的权重
        diffMat = testPoint - xMat[j, :]
        weights[j, j] = np.exp(diffMat * diffMat.T / (-2.0 * k ** 2))
    xTx = xMat.T * (weights * xMat)
    if np.linalg.det(xTx) == 0.0:
        print("矩阵为奇异矩阵,不能求逆")
        return
    ws = xTx.I * (xMat.T * (weights * yMat))  # 计算回归系数
    return testPoint * ws

def lwlrTest(testArr, xArr, yArr, k=1.0):
    '''
    局部加权线性回归测试
    :param testArr: 测试数据集
    :param xArr: 数据集
    :param yArr: 标签y
    :param k:高斯核的k,自定义参数
    :return:回归系数向量
    '''
    m = np.shape(testArr)[0]  # 计算测试数据集大小
    yHat = np.zeros(m)
    for i in range(m):  # 对每个样本点进行预测
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)
    return yHat

if __name__ == '__main__':
    plotlwlrRegression()

可以看出当k越小（比如k=0.01），拟合效果越好。但是k=0.003时过小，导致考虑了太多噪声，进而导致了过拟合现象。

五、岭回归

上面提到，计算回归参数需要保证X^TX可逆（满秩）。那么如果数据的特征点比样本数还多，那么矩阵X肯定不是满秩矩阵，无法求逆，导致无法使用正常的线性回归。因此统计学家引入岭回归（ridge regression）的概念。

定义

岭回归就是在矩阵X^TX上加一个λI从而使得矩阵非奇异，进而能对X^TX + λI求逆。其中矩阵I是一个m×m的单位矩阵，对角线上元素全为1，其他元素全为0。而λ是一个用户定义的数值。回归系数的计算公式将变成：

θ=(XTX+λI)−1XTy \theta = (X^T X + \lambda I)^{-1} X^T y

这里通过引入λ来限制了所有θ之和，通过引入该惩罚项，能减少不重要的参数，这个技术在统计学中叫做缩减(shrinkage)

六、梯度上升和梯度下降

梯度上升（下降）法基于的思想是:要找到某函数的最大（小）值，最好的方法是沿着该函数的梯度方向探寻。函数f(x,y)的梯度由下面公式表示:

∇(x,y)=(∂f(x,y)∂x∂f(x,y)∂y) \nabla(x,y)=\begin{pmatrix} \dfrac{\partial{f(x,y)}}{\partial{x}} \\ \dfrac{\partial{f(x,y)}}{\partial{y}} \end{pmatrix}

梯度是三维以上坐标系的概念，它在平面坐标系对应的概念是导数。二维平面中，导数代表线的倾斜方向和倾斜程度。三维空间中，梯度代表 面的倾斜方向和倾斜程度。线的倾斜方向只用正负表示，导数为正代表右斜，导数为负代表线左斜。面的倾斜方向是无穷的，由向量表示。

梯度上升和梯度下降，指的是你要计算的结果是函数的极大值还是极小值。计算极小值，就用梯度下降，计算极大值，就是梯度上升。

梯度上升

梯度上升的算法如下：

w:=w+α∇wf(w) w := w+ \alpha \nabla_w{f(w)}

可以根据简化的二维平面y=-x^2函数来求最大值来理解，当x<0时导数为正，函数值在0时最大。

  • 当取w<0时，导数为正，因此迭代后的w会往右侧（最大值所在的x=0）靠近。
  • 当取w>0时，导数为负，因此迭代后的w会往左侧（最大值所在的x=0）靠近。

梯度下降

梯度下降的算法如下：

w:=w−α∇wf(w) w := w- \alpha \nabla_w{f(w)}

可以根据简化的二维平面y=x^2函数来求最小值来理解，当x>0时导数为正，函数值在0时最小。

  • 当取w<0时，导数为负，因此迭代后的w会往右侧（最大值所在的x=0）靠近。
  • 当取w>0时，导数为正，因此迭代后的w会往左侧（最大值所在的x=0）靠近。

当三维甚至多维时，w变成向量。

当矩阵不满秩时，可采用梯度下降算法来求局部最优解的方法。

七、Logistic回归和Sigmoid函数的分类

我们想要的函数应该是，能够接受所有的输入然后预测出类别。例如在两个类的情况下，分类函数能够输出0或1，这种函数称为“海威赛德阶跃函数”，然而这个函数的问题在于，该函数直接在跳跃点从0跳跃到1，这个瞬间的跳跃有点难处理。

ϵ(t−t0)={1if t>t00if t<t0 \epsilon(t-t_0)=\begin{cases} 1 &\text{if } t>t_0 \\ 0 &\text{if } t<t_0 \end{cases}

幸好有个函数有类似的性质，并且在数据上更容易处理，这就是Sigmoid函数：

g(z)=11+e−z g(z)=\dfrac{1}{1+e^{-z}}

该函数的特性为：当x趋近于负无穷时，y趋近于0；当x趋近于正无穷时，y趋近于1；当x= 0时，y=0.5。

回归系数

为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5被归入0类。所以，Logistic回归也可以被看成是一种概率估计。

什么是回归系数呢？可由下面公式得出

z=w0x0+w1x1+w2x2+...+wnxn z=w_0x_0+w_1x_1+w_2x_2+...+w_nx_n

向量写法如下，其中向量x是分类器的输入数据，向量w就是回归系数。

z=[x0,x1,...,xn][w1w2⋮wn]=xwT z=[x_0,x_1,...,x_n] \begin{bmatrix} w_{1} \\ w_{2} \\ \vdots \\ w_{n} \\ \end{bmatrix} = x w^T

损失函数的模型建立

根据z和g(z)公式，得出：

hw(x)=g(wTx)=11+e−wTx h_w(x)=g(w^Tx)=\dfrac{1}{1+e^{-w^Tx}}

w是需要求解的参数向量，x是样本的数据集，hw(x) h_w(x)函数实现了任意实数到[0,1]的映射，代表了输出为1的概率，当hw(x) h_w(x)=0.6时，说明有60%的概率输出为1，40%的概率输出为0。即P(y=1|x,w)=hw(x) h_w(x)和P(y=0|x,w)=1−hw(x) 1-h_w(x)

我们需要的是一个代价函数，使得样本要么是0，要么是1的概率更高，代表分类效果越好。因此构建出代价函数：

Cost(hw(x),y)=(hw(x))y(1−hw(x))1−y Cost(h_w(x),y)=(h_w(x))^y (1-h_w(x))^{1-y}

当y=1时，(1-y)为0；当y=0时，(1-y)为1，保证只保留两项中的一项。然后取对数简化：

Cost(hw(x),y)=ylog(hw(x))+1−ylog(1−hw(x)) Cost(h_w(x),y)=y \log{(h_w(x))} + {1-y} \log{(1-h_w(x))}

对于某个数据集，由于样本之间相互独立，整个数据集的概率，是所有样本概率的乘积，我们也同样对数化（同时也由于很小的数相乘导致下溢出），每个样本的值越大，代表是0或者1的可能性越大，则分类越准确。问题变成求解如下代价函数J(w)的最大值问题。

J(w)=∑i=1m[y(i)log(hw(x(i)))+1−y(i)log(1−hw(x(i)))] J(w)=\sum_{i=1}^m [y^{(i)} \log{(h_w(x^{(i)}))} + {1-y^{(i)}} \log{(1-h_w(x^{(i)}))}]

其中，m为样本的总数，y(i)表示第i个样本的类别，x(i)表示第i个样本，需要注意的是w是多维向量，x(i)也是多维向量。

最佳回归系数的数学推导

求损失函数最大值，我们需要使用梯度上升算法。公式为：

wj:=wj+α∂J(w)wj w_j := w_j + \alpha \dfrac{\partial J(w)}{w_j}

现在开始求解J(w)对w的偏导：

∂wjJ(w)=∂J(w)∂g(wTx)×∂g(wTx)∂wTx×∂wTx∂wj \dfrac{\partial}{w_j} J(w) = \dfrac{\partial J(w)}{\partial g(w^Tx)} \times \dfrac{\partial g(w^Tx)}{\partial w^Tx} \times \dfrac{\partial w^Tx}{\partial w_j}

三者都需要计算，较为复杂，最后会得到

∂wjJ(w)=(y−hw(x))xj\dfrac{\partial}{w_j} J(w) =(y-h_w(x))x_j

最终得到梯度上升的迭代公式为：

wj:=wj+α∑i=1m(y(i)−hw(x(i)))xj(i)w_j := w_j+ \alpha \sum_{i=1}^m (y^{(i)}-h_w(x^{(i)}))x_j^{(i)}

八、逻辑回归分类示例

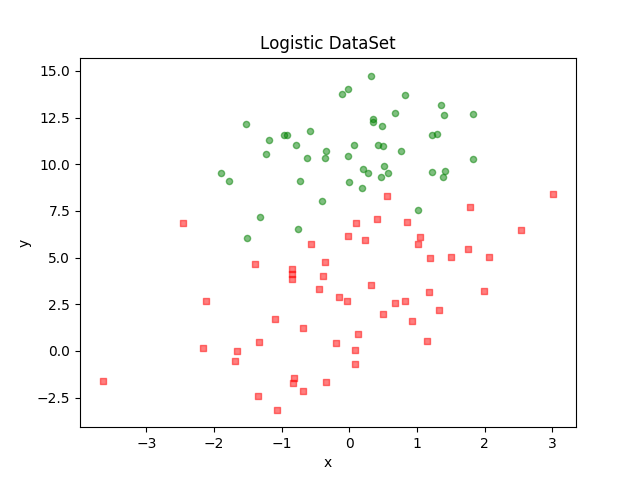
有数据如下，包含两维特征，训练逻辑回归分类。

x轴 y轴 分类标签
-0.017612 14.053064 0
-1.395634 4.662541 1
… … …
0.423363 11.054677 0
0.406704 7.067335 1
0.667394 12.741452 0

准备数据、可视化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
import matplotlib.pyplot as plt

def loadDataSet():
    '''
    读取数据集
    :return:数据集和分类标签
    '''
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def plotDataSet():
    '''
    数据可视化
    :return:
    '''
    dataMat, labelMat = loadDataSet()                                    #加载数据集
    dataArr = np.array(dataMat)                                            #转换成numpy的array数组
    n = np.shape(dataMat)[0]                                            #数据个数
    xcord1 = []; ycord1 = []                                            #正样本
    xcord2 = []; ycord2 = []                                            #负样本
    for i in range(n):                                                    #根据数据集标签进行分类
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])    #1为正样本
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])    #0为负样本
    fig = plt.figure()
    ax = fig.add_subplot(111)                                            #添加subplot
    ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)#绘制正样本
    ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5)            #绘制负样本
    plt.title('Logistic DataSet')                                                #绘制title
    plt.xlabel('x'); plt.ylabel('y')                                    #绘制label
    plt.show()

需要使用逻辑回归进行分类

梯度向上算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def sigmoid(inX):
    '''
    sigmoid函数映射
    :param inX:参数
    :return:函数值y，即为1的概率
    '''
    return 1.0/(1+np.exp(-inX))

def gradAscent(dataMatIn, classLabels):
    '''
    梯度上升算法
    :param dataMatIn:数据集
    :param classLabels:分类标签
    :return:
    '''
    dataMatrix = np.mat(dataMatIn)             #转换为矩阵
    labelMat = np.mat(classLabels).transpose() #转换为矩阵并转置
    m,n = np.shape(dataMatrix)              #获取数据集矩阵大小
    alpha = 0.001                           #步长
    maxCycles = 500                         #迭代次数
    weights = np.ones((n,1))                #初始w回归系数，默认都为1
    for k in range(maxCycles):              #迭代
        h = sigmoid(dataMatrix*weights)
        error = (labelMat - h)
        weights = weights + alpha * dataMatrix.transpose()* error #根据梯度上升算法，逐渐优化w回归系数
    return weights #返回500次迭代后的最优w回归系数

测试

1
2
3
4
if __name__ == '__main__':
    dataMat, labelMat = loadDataSet()
    weights = gradAscent(dataMat, labelMat)
    plotBestFit(weights)

结果为：

1
2
3
[[ 4.12414349]
 [ 0.48007329]
 [-0.6168482 ]]

结果可视化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()  # 加载数据集
    dataArr = np.array(dataMat)  # 转换成numpy的array数组
    n = np.shape(dataMat)[0]  # 数据个数
    xcord1 = []
    ycord1 = []  # 正样本
    xcord2 = []
    ycord2 = []  # 负样本
    for i in range(n):  # 根据数据集标签进行分类
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i, 1]);
            ycord1.append(dataArr[i, 2])  # 1为正样本
        else:
            xcord2.append(dataArr[i, 1]);
            ycord2.append(dataArr[i, 2])  # 0为负样本
    fig = plt.figure()
    ax = fig.add_subplot(111)  # 添加subplot
    ax.scatter(xcord1, ycord1, s=20, c='red', marker='s', alpha=.5)  # 绘制正样本
    ax.scatter(xcord2, ycord2, s=20, c='green', alpha=.5)  # 绘制负样本
    x = np.arange(-3.0, 3.0, 0.1)
    y = (-weights[0,0] - weights[1,0] * x) / weights[2,0]
    ax.plot(x, y)
    plt.title('BestFit')  # 绘制title
    plt.xlabel('X1')
    plt.ylabel('X2')  # 绘制label
    plt.show()

九、回归相关代码

『代码传送门』

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true